+ 86-18052080815 | info@harsle.com
Anzahl Durchsuchen:1108 Autor:Site Editor veröffentlichen Zeit: 2024-08-30 Herkunft:Powered
Die Berechnung des korrekten flachen Musterlayouts ist entscheidend, um ein qualitativ hochwertiges Fertigteil von Ihrem Unternehmen zu erhalten Abkantpresse. Dennoch haben viele CAD- und CNC-Programmierer keine Ahnung, wie sie die erforderlichen Werte berechnen sollen. Vor Jahren erstellten echte Experten Spickzettel und hefteten sie an die Wand. Sie brachten dem neuen Lehrling nur bei, wie man die auf dem Spickzettel angezeigten Ergebnisse anwendet, nicht aber, wie man die Zahlen berechnet. Nun sind diese Experten in den Ruhestand getreten und es ist an der Zeit, dass eine neue Generation lernt, wie man das richtige flache Musterlayout richtig berechnet.
Die Berechnung der Abwicklungslänge aus dem 3D-Teil ist eigentlich gar nicht so schwierig. Obwohl Sie möglicherweise mehrere verschiedene Formeln finden, die dies behaupten Berechnen Sie die Biegezugabe (Siehe Biegedefinitionen), es handelt sich normalerweise um dieselbe Formel, nur vereinfacht durch Eingabe des Winkels oder eines K-Faktors. Oh, und ja, Sie müssen den K-Faktor kennen, um die Biegezugabe zu berechnen.

Beginnen wir mit einer einfachen L-Klammer. Das Bild zeigt, dass die Beine der Halterung 2 Zoll und 3 Zoll groß sind. Die Materialstärke beträgt 0,125 Zoll, der Innenradius beträgt 0,250 Zoll und der Biegewinkel beträgt 90 Grad. Die flache Länge ist die Summe aus dem flachen Teil beider Flansche plus der Länge durch den Bogen des Biegebereichs. Aber berechnen Sie das auf der Innenseite des Materials oder auf der Außenseite? Weder! Hier kommt der K-Faktor ins Spiel. Der K-Faktor ist der Prozentsatz der Materialdicke, bei dem es zu keiner Dehnung oder Stauchung des Materials kommt, beispielsweise auf der neutralen Achse. Für diese einfache L-Klammer verwende ich einen K-Faktor von 0,42.

Die Formel (siehe Biegeformeln) lautet:
Biegezugabe = Winkel * (π / 180) * (Radius + K-Faktor * Dicke).
Wenn wir unsere Zahlen einsetzen, erhalten wir: Biegezugabe = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475'
Die Länge des flachen Musters beträgt also 1,625 Zoll + 2,625 Zoll + 0,475 Zoll, was 4,725 Zoll entspricht. Wenn Sie also die flache Länge aller Flansche addieren und für jeden Biegebereich eine Biegezugabe hinzufügen, erhalten Sie die korrekte flache Länge des Teils.
Aber schauen Sie sich die Zeichnung an. Normalerweise dimensionieren wir ein Blechteil nicht so. Die Abmessungen beziehen sich normalerweise auf den Schnittpunkt der Flansche oder die Formlinie. Das bedeutet, dass wir für jeden Biegebereich das Zweifache der Materialstärke plus den Biegeradius (auch Setback genannt) abziehen müssen. Für diesen Bemaßungssatz wäre es einfacher, den Biegekompensationswert zu berechnen. Mit dem Biegekompensationswert können Sie die Länge jedes Flansches mithilfe der Formlinienabmessungen addieren und dann eine Biegekompensation pro Biegebereich zur Gesamtsumme hinzufügen. Es ist -0,275, eine negative Zahl, was bedeutet, dass Sie diesen Betrag von der Gesamtlänge der Flansche, 5 Zoll, abziehen, um 4,725 Zoll zu erhalten.
Biegezugabe = Winkel * (π / 180) * (Radius + K-Faktor * Dicke)
Biegekompensation = Biegezugabe – (2 * Zurücksetzen)
Innenversatz = tan (Winkel / 2) * Außenradius
Zurücksetzen = tan (Winkel / 2) * (Radius + Dicke)

Biegezugabe – Die Länge des Bogens durch den Biegebereich an der neutralen Achse.
Biegewinkel – Der eingeschlossene Winkel des durch den Biegevorgang gebildeten Bogens.
Biegekompensation – Der Betrag, um den das Material durch den Biegevorgang gedehnt oder gestaucht wird. Es wird davon ausgegangen, dass jegliche Dehnung oder Kompression im Biegebereich auftritt.
Biegelinien – Die geraden Linien auf der Innen- und Außenfläche des Materials, wo die Flanschgrenze auf den Biegebereich trifft.
Innenbiegeradius – Der Radius des Bogens auf der Innenfläche des Biegebereichs.
K-Faktor – Definiert die Position der neutralen Achse. Sie wird als Abstand von der Innenseite des Materials zur neutralen Achse dividiert durch die Materialdicke gemessen.
Formlinien – Bei Biegungen von weniger als 180 Grad sind die Formlinien die geraden Linien, an denen sich die den Biegebereich begrenzenden Flanschflächen schneiden. Dies geschieht sowohl an der Innen- als auch an der Außenfläche der Biegung.
Neutrale Achse – Betrachtet man den Querschnitt der Biegung, ist die neutrale Achse der theoretische Ort, an dem das Material weder gestaucht noch gedehnt wird.
Zurücksetzen - Bei Biegungen von weniger als 180 Grad ist der Abstand der Abstand zwischen den Biegelinien und der Formlinie.
Meines Wissens gibt es keine Formel zur Berechnung des k-Faktors. Oh, ich bin mir sicher, dass irgendein Mathematiker irgendwo eine Formel hat. Aber es ist höchstwahrscheinlich zu komplex, als dass die meisten von uns es verstehen oder nutzen könnten.
Der k-Faktor ist der Prozentsatz der Materialstärke, bei dem es im Biegebereich zu keiner Dehnung oder Stauchung des Materials kommt. Also die neutrale Achse!
Je härter das Material, desto geringer ist die Kompression an der Innenseite der Biegung. Daher erfolgt eine stärkere Dehnung an der Außenseite und die neutrale Achse bewegt sich in Richtung der Innenseite der Biegung. Weichere Materialien ermöglichen eine stärkere Kompression im Inneren und die neutrale Achse bleibt näher an der Mitte der Materialstärke.
Der Biegeradius hat einen ähnlichen Effekt. Je kleiner der Biegeradius, desto größer ist der Druckbedarf und die neutrale Achse verschiebt sich in Richtung der Innenseite der Biegung. Auf einem größeren Radius. die neutrale Achse bleibt in der Nähe der Mitte der Materialdicke.

Um Ihnen dabei zu helfen, die Berechnungsformel für die ausgestreckte Biegelänge einfacher und schneller zu beherrschen, haben wir für Sie vier gängige Koeffiziententabellen aufgelistet, sechzehn Berechnungsformeln für die ausgestreckte Biegelänge illustriert und zum besseren Verständnis auch einige Beispiele aufgeführt. Ich hoffe, dass die folgenden Inhalte Ihnen praktisch weiterhelfen können. Wenn Sie Fragen haben, können Sie sich gerne an uns wenden.






A, B --- Biegelänge des Werkstücks
P'---Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die erweiterte Länge L=A+B-P', also L=25+65-5,5=84,5
Gemäß Tabelle 1 beträgt die Plattendicke 3, die untere Matrize V25 und der Biegekoeffizient 5,5
Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

A(A1), B--- Biegelänge des Werkstücks
P'---Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die erweiterte Länge L=A+T+B-2*P', also L=50+2+50-2*3,4=95,2
Gemäß Tabelle 1 beträgt die Plattendicke 2, die untere Matrize V12 und der Biegekoeffizient 3,4
Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

A(A1), B (B1)-Biegelänge des Werkstücks
P'---Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die erweiterte Länge L=A+T+B+T-3*P', also L=50+2+90+2-3*3,4=133,8
Gemäß Tabelle 1 beträgt die Plattendicke 2, die untere Matrize V12 und der Biegekoeffizient 3,4
Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

A, B (B1) – Biegelänge des Werkstücks
P'---Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die erweiterte Länge L=A+A+B+T+T-4*P', also l = 25+25+100+1,5+1,5-4 * 2,8 = 141,8
Gemäß Tabelle 1 beträgt die Plattendicke 1,5, die untere Matrize V12 und der Biegekoeffizient 2,8
Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

A(A1), B (B1)-Biegelänge des Werkstücks
P'---Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die Erweiterungslänge L=A+T+A+T+B+B1+B1-6*P'
Das ist l = 50+1,5+50+1,5+150+20+20-6 * 2,8 = 276,2
Gemäß Tabelle 1 beträgt die Plattendicke 1,5, die untere Matrize V12 und der Biegekoeffizient 2,8
Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

A, B --- Biegelänge des Werkstücks
P'---Biegekoeffizient der Abflachungskehle
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die erweiterte Länge L=A+B-P', also L=25+65-1=89
Gemäß Tabelle 2 beträgt die Plattendicke 2, das Unterwerkzeug V12 und der Biegefaktor die Hälfte der Plattendicke
Hinweis: Gemäß Tabelle 2 hat die Auswahl verschiedener Unterwerkzeuge unterschiedliche Biegekoeffizienten und unterschiedliche Plattendicken zur Folge.
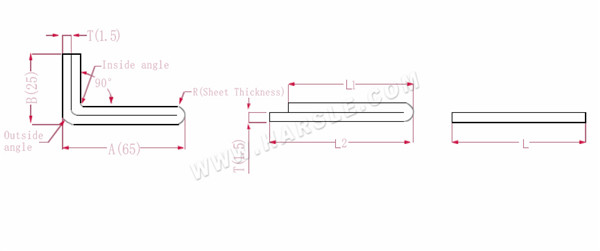
A, B --- Biegelänge des Werkstücks
P1--- Biegekoeffizient der Innenecke
P2--- Biegekoeffizient des äußeren Biegewinkels
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die erweiterte Länge L1=(A-1,5) +(B-1,5)-P1, also L1= (65-1,5) +(25-1,5)-3,2=83,8
L2=A+B-P2, also L2=65+25-4,1=85,9
L=L1+L2-T/2, also L=83,8+85,9-0,75=168,95
Gemäß Tabelle 2 beträgt die Plattendicke 1,5, die untere Matrize ist V12, der Biegekoeffizient der inneren Ecke beträgt 3,2, der Biegekoeffizient der äußeren Ecke beträgt 4,1 und der Biegekoeffizient von 180 beträgt 0,75.
Hinweis: Gemäß Tabelle 2 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.
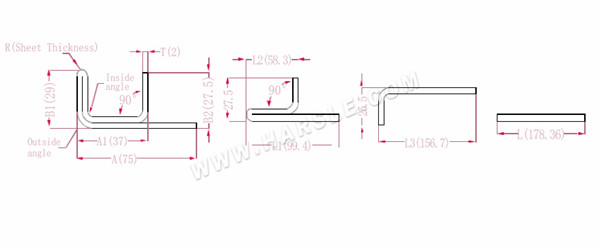
A, A1, A2, B1, B2, L, L1, L2, L3--- Biegelänge des Werkstücks
P1--- Biegekoeffizient der Innenecke
P2--- Biegekoeffizient des äußeren Biegewinkels
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die erweiterte Länge L1=(A1-T) +(B2-T)-P1 ist L1= (35-2) +(34-2)-3,7=61,3
L2=(B1-T) +(A2-T)-P1, was L2= (50-2) +(34-2)-3,7=76,3 ist
L3=A+B1+B2-2*P2, also L3=70+35+50-2*4,6+145,8
L=L1+L2+L3-2*P3, also L=61,3+75,3+145,8-2*1=280,4
Gemäß Tabelle 2 beträgt die Plattendicke 2, die untere Matrize ist V12, der Innenecken-Biegekoeffizient beträgt 3,7, der Außenecken-Biegekoeffizient beträgt 4,6 und der 90-Biegekoeffizient beträgt 1.
Hinweis: Gemäß Tabelle 2 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.
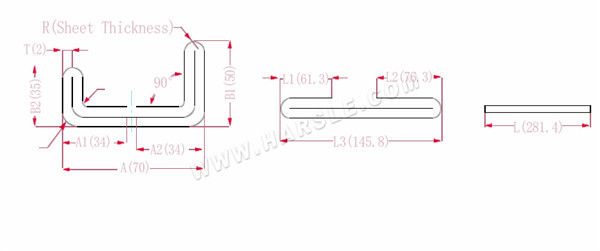
A, A1, A2, B1, B2, L, L1, L2, L3--- Biegelänge des Werkstücks
P1--- Biegekoeffizient der Innenecke
P2--- Biegekoeffizient des äußeren Biegewinkels
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die erweiterte Länge L1=(A1-T) +(B2-T)-P1, also L1= (35-2) +(34-2)-3,7=61,3
L2=(B1-T) +(A2-T)-P1, was L2= (50-2) +(34-2)-3,7=76,3 ist
L3=A+B1+B2-2*P2, also L3=70+35+50-2*4,6+145,8
L=L1+L2+L3-2*P3, also L=61,3+75,3+145,8-2*1=280,4
Gemäß Tabelle 2 beträgt die Plattendicke 2, die untere Matrize ist V12, der Innenecken-Biegekoeffizient beträgt 3,7, der Außenecken-Biegekoeffizient beträgt 4,6 und der 90-Biegekoeffizient beträgt 1.
Hinweis: Gemäß Tabelle 2 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.
Diagramm und Berechnungsformel des Stufenbiegens
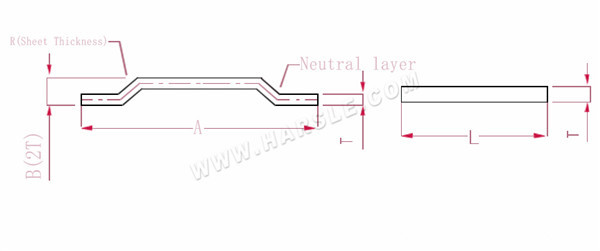
A, B --- Biegelänge des Werkstücks
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Entfaltete Länge L=A+1
Hinweis: Wenn die Stufe der Dicke von zwei Platten entspricht, addieren Sie 0,5 für jede Stufe und 1 für jede Stufe.
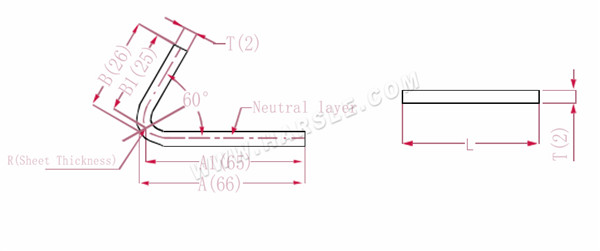
A(A1), B (B1)-Biegelänge des Werkstücks
P'---Biegekoeffizient der Kantenbiegung (Biegefaktor: ein Faktor minus eine Biegung)
R---Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die Erweiterungslänge L=(AT) +(BT)-P', also L= (66-1) +(26-1)-2=65+25-2=88
Gemäß Tabelle 3 beträgt die Plattendicke 2, die untere Matrize V12 und der 60-Biegekoeffizient 2
Hinweis: Gemäß Tabelle 3 wird die neutrale Schicht als Biegelänge und -breite ausgewählt.
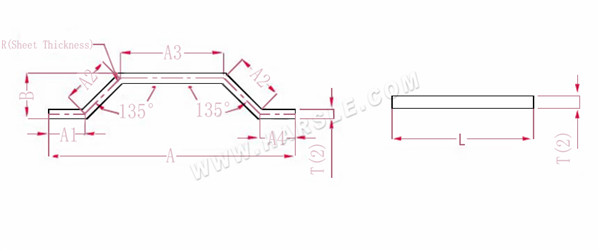
A (A1, A2, A3, A4), B--- Biegelänge des Werkstücks
P--- Biegefaktor von 135 Biegewinkeln
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Die Ausdehnungslänge L = A1+A2+A3+A2+A4-PP.
Hinweis: Bei derselben Druckstufenbiegung müssen nur zwei Koeffizienten reduziert werden
Gemäß Tabelle 3: Die Plattendicke beträgt 2, die untere Matrize ist V12 und der Biegekoeffizient bei 135 beträgt 1,1.
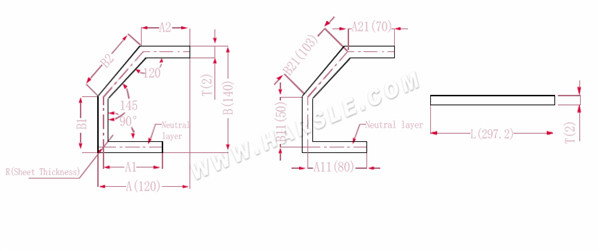
A (A1, A2), B (B1, B2) – Biegelänge des Werkstücks
P1---120° Biegekoeffizient
P2---145° Biegekoeffizient
P3---90° Biegekoeffizient
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
Hinweis: Wenn die Grafikgröße auf der Form markiert ist, sollte die Formgröße bei der Berechnung der Entfaltungslänge in die neutrale Ebenengröße umgewandelt werden;
Die Ausdehnungslänge L=A11+B11+B21+A21-P1-P2-P3 beträgt l = 80+50+103+70-1,7-0,7-3,4 = 297,2
Gemäß Tabelle 3 beträgt die Plattendicke 2, die untere Matrize ist V12, der 120-Biegekoeffizient beträgt 1,7, der 145-Biegekoeffizient beträgt 0,7 und der 90-Biegekoeffizient beträgt 3,4
Hinweis: Gemäß Tabelle 3 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.
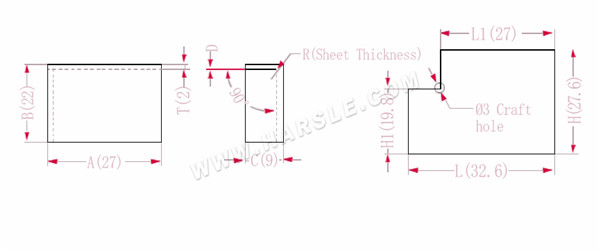
A, B, C --- Länge, Breite und Höhe der Biegekante des Werkstücks
P --- Biegekoeffizient
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
H(H1), l (L1) – die entfaltete Länge jeder Seite
T--- Materialstärke
D --- Biegeprozessspiel (im Allgemeinen 0 ~ 0,5)
Die erweiterte Länge L1=A, also L1=27
L=A+CP, also L=27+9-3,4=32,6
H1=BTD, also H1=22-2-0,2=19,8. Hinweis: D ist 0,2.
H=B+CP, also H=22+9-3,4=27,6
Gemäß Tabelle 1 beträgt die Blechdicke 2, die untere Matrize V12 und der Biegekoeffizient 3,4
Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.
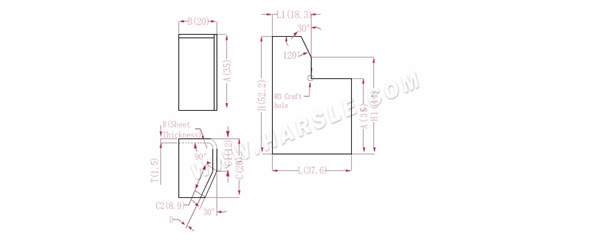
A, B, C --- Länge, Breite und Höhe der Biegekante des Werkstücks
H(H1), L (L1) – die entfaltete Länge jeder Seite
P---90° Biegekoeffizient P1---30° Biegekoeffizient
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
D --- Biegeprozessspiel (im Allgemeinen 0 ~ 0,5)
Die erweiterte Länge L1=BTD, also L1=20-1,5-0,2=18,3
L=B+C1+C2-P-P1, also L=20+12+8,9-2,8-0,5=37,6
H1=C1+APD, also H1=12+35-2,8-0,2=44. Hinweis: D ist 0,2.
H=A+CP, also H=35+20-2,8=52,2
Gemäß Tabelle 1: Die Plattendicke beträgt 1,5, die untere Matrize ist V12, der Biegekoeffizient beträgt 2,8 und der 30-Biegekoeffizient beträgt 0,5
Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.

A, B, C --- Länge, Breite und Höhe der Biegekante des Werkstücks
H(H1), L (L1) – die entfaltete Länge jeder Seite
P --- Biegekoeffizient
R--- Biegung und Verrundung (im Allgemeinen Blechdicke)
T--- Materialstärke
D --- Biegeprozessspiel (im Allgemeinen 0 ~ 0,5)
Die erweiterte Länge H1=B-B1-D, also H1=50-12-0,3=37,7. Hinweis: D ist 0,2.
H2=BTD, also H2=50-2,5-0,3=47,2
H=B+C+B1-2*P, also H=50+47+12-2*4,5=100
L1=A+CTDP, also L1=55+47-2,5-0,3-4,5=94,7
L=A+C+B2-2*P, also L=55+47+12-2*4,5=105
Laut Tabelle 1 beträgt die Blechdicke 1,5, das Unterwerkzeug V16 und der Biegekoeffizient 4,5
Hinweis: Gemäß Tabelle 1 sind unterschiedliche Biegekoeffizienten der Unterwerkzeuge und unterschiedliche Plattendicken unterschiedlich.